.png)
Chapitre 7 : Statistique.
I. Rappel
- Population statistique c’est l’ensemble des éléments étudié.
- Un caractère : c’est la propriété étudiée (𝒙𝒊).
1- Quantitatif (on peut le mesurer).
2- Qualitatif (il ne se mesure pas).
- Effectif : Effectif d’une valeur est le nombre de fois que cette valeur est répétée (𝒏𝒊).
- Effectif cumulé : Effectif cumulé d’une valeur est la somme de l’effectif de cette valeur avec les précédentes.
- Effectif total : est égal La somme des effectifs (𝑵).
- Fréquence : la fréquence d’une valeur
- Fréquence cumulée : Fréquence cumulée est le rapport de l’effectif cumulé correspond à cette valeur et l’effectif totale.
- Pourcentages :
II. Tableau des effectifs, des effectifs cumulés, des fréquences et des fréquences cumulées.
1- Série statistique en valeurs :
La série statistique se présente sous la forme d’une liste de valeurs, par exemple : 1 – 10 – 20 – 50.
Remarque : On classe la série par ordre croissant.
a. Exemple 1.
Le tableau suivant donne une classification des matières enseignées dans le deuxième collège, selon ses coefficients :
b. Exemple 2.
2- Série statistique en classes :
a. Exemple 3.
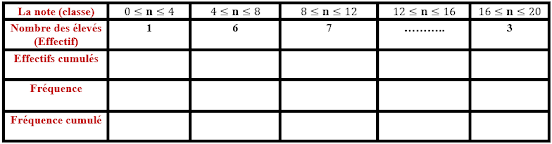
Le tableau suivant donne les notes obtenues par 25 élevés au dernier devoir de contrôle continu :
III- Moyenne arithmétique :
a. Définition .
Pour obtenir la moyenne d’une série statistique :
- On multiplie chaque valeur (ou centre de classe) par l’effectif correspondant.
- On additionne les produits ainsi obtenus.
- On divise cette somme par l’effectif total.
b. Remarque .
Dans le cas d’une série statistique en classes, en calculant d’abord le centre de chaque classe. Pour déterminer la moyenne.
Le centre de classe a ≤ 𝒙 ≤ b est le nombre : (a + b)/2 .
c. Exemple 1.
Série statistique en valeurs.
Calculons la moyenne arithmétique de la série statistique suivante :
m = ( 1 × 3 + 2 × 2 + 3 × 2 + 5 × 3 ) / 10
m = ( 3 + 4 + 6 + 15 ) / 10
m = 28 / 10
m = 2.8
La moyenne arithmétique de cette série statistique est : 2.8
d. Exemple 2.
Calculons la moyenne arithmétique de la série statistique suivante :
m = ( 1 × 2 + 6 × 6 + 7 × 10 + 8 × 14 + 3 × 18 ) / 25
m = ( 2 + 36 + 70 + 112 + 54 ) / 25
m = 274 / 25
m = 11
La moyenne arithmétique de cette série statistique est : 11
IV- Le mode d'une série Statistique :
a. Définition .
Le mode d'une série statistique est la valeur du caractère qui a le plus grand effectif.
b. Exemple 1
Quel est le mode de cette série statistique ?
On a le plus grand effectif est :16 qui correspond à la valeur : 9
Donc le mode de cette série statistique est : 9
c. Exemple 2.
Quel est le mode de cette série statistique ?
Donc le mode (la classe modal) de cette série statistique se trouve dans la classe : 3 ≤ 𝒙 ≤ 4
V- La Médiane d'une série Statistique :
a. Définition .
On appelle médiane d’une série statistique, dont les valeurs sont ordonnées, tout nombre qui partage cette série en deux groupes de même effectif.
b. Exemple 1
(l’effectif total est un nombre impair).
On considère la série statistique suivante triée par ordre croissant :
1 - 2 - 2 - 3,5 - 5 - 7 - 7 - 7,5 - 8
c. Exemple 2.
On considère la série statistique suivante triée par ordre croissant :
1 - 2 - 2 - 5 - 7 - 7 - 8 - 8
On a : = ( 5 + 7 ) / 2 = 12 / 2 = 6
La médiane de cette série statistique est : 6
d. Application
On considère la série statistique suivante :
19 ; 16 ; 9,5 ; 14 ; 7 ; 10 ; 12 ; 9,5 ; 9 ; 16 ; 10
Déterminer la médiane de cette série.
Correction :
On classe la série statistique par ordre croissant :
e. Définition 2.
La médiane est la plus petite valeur du caractère dont l’effectif cumulé supérieur ou égal à la moitié de l’effectif total N.
b. Exemple 1.
Calculons la médiane de la série statistique suivante :
La moitié de l’effectif total N est : 10 / 2 = 5
Donc le plus petit effectif cumulé supérieur ou égal à 5 est 5 qui correspond à la valeur : 2
Donc La médiane de cette série statistique est : 2
c. Exemple 2.
.Série statistique en classes
Calculons la médiane de la série statistique suivante :
Donc le plus petit effectif cumulé supérieur ou égal à 12.5 est 14 qui correspond à la classe : 8 ≤ 𝐧 ≤ 12 Donc La médiane de cette série statistique se trouve dans la classe : 8 ≤ 𝐧 ≤ 12
VI- La dispersion : :
a. Définition .
On considère deux séries statistiques 𝑆1 et 𝑆2 de même moyenne arithmétique m.
𝑆1 et moins dispersée que 𝑆2 signifie que les valeurs du caractère de 𝑆1 sont près à la moyenne m que les valeurs de 𝑆2.
b. Exemple .
Dans le tableau suivant les notes de cinq devoirs de deux élèves Ahmed et Omar :
La moyenne d’Ahmed est : m1 = ( 9 + 14 + 10 + 13 + 14) / 5 = 12
La moyenne d’Omar est : m2 = ( 8 + 16 + 10 + 17 + 9) / 5 = 12
Donc m 1 = m 2 Alors ils ont la même moyenne Et on a les notes d’Ahmed sont près à la moyenne que les notes de d’Omar. On dit alors que les notes d’Ahmed sont moins dispersées que les notes d’Omar.1- الدرس على شكل PDF:
"الإحصاء" بصيغة PDF ، ستجد الملف الآن للاستفادة من الشرح المبسط والأمثلة العملية.
2- شرح فقرات الدرس بالفيديو على قناتي في اليوتيوب:
لجعل عملية الفهم أسهل وأكثر تفاعلية، نقدم لك سلسلة من الفيديوهات التي تشرح كل فقرة من الدرس بشكل مفصل ومبسط.- I- Rappel
- II- Tableau des effectifs, des effectifs cumulés, des fréquences et des fréquences cumulées
- تذكير
- جدول الحصيصات، جدول الحصيصات المتراكمة، جدول الترددات، جدول الترددات المتراكمة.
3- التمارين : les exercices
في هذا الفيديوهات ستجد شرح مبسط ومفهوم بطريقة بسيطة لسلسة التمارين :4- 📢 حمّل تطبيق MATHS 3APIC الآن! 📢
هل أنت تلميذ في السنة الثالثة إعدادي وتبحث عن أفضل طريقة لإتقان الرياضيات؟ لا داعي للبحث أكثر! MATHS 3APIC هو التطبيق المثالي لك.🔹 دروس – شروحات واضحة وبسيطة لجميع المواضيع.
🔹 تمارين – تدرب على مجموعة متنوعة من الأسئلة.
🔹 امتحانات – اختبر نفسك واستعد للنجاح!
👉 حمّل تطبيق MATHS 3APIC الآن وطور مهاراتك في الرياضيات! 🚀